概述

最短路径研究的是在一幅加权有向图中，所有从顶点 s 到顶点 t 的路径中的权值最小者。如下图红线圈起来就是权值更小的路径。

加权有向图的数据结构

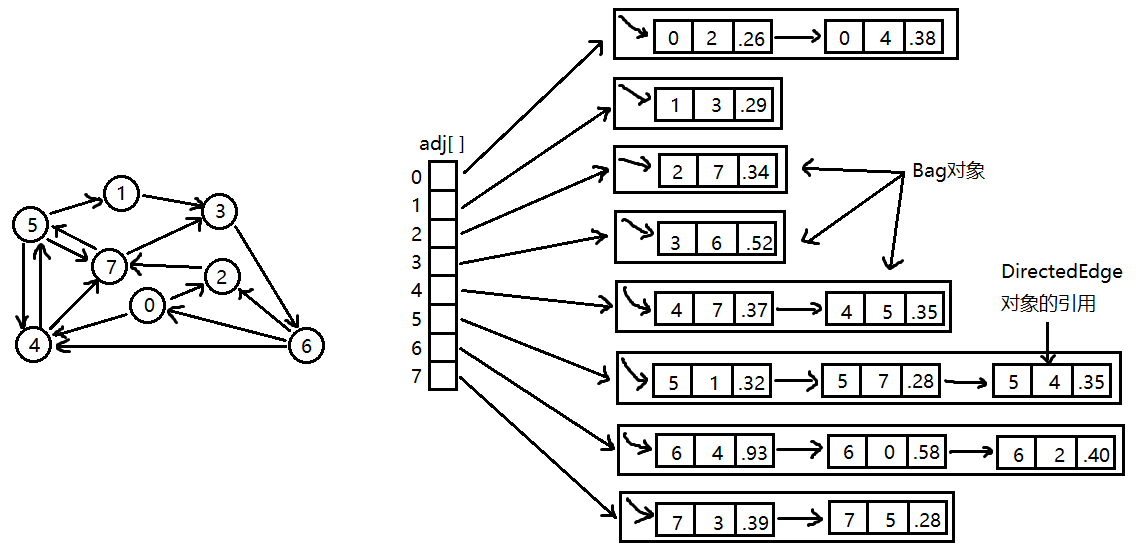
加权有向图的数据结构比加权无向图更加简单，因为有向边只有一个方向。所以与 Edge 类中的 either() 和 other() 方法不同，这里定义了 from() 与 to() 方法。

DirectedEdge 类

public class DirectedEdge {
    private final int v;         // 边的起点
    private final int w;         // 边的终点
    private final double weight; // 边的权重

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }
    public double weight() {
        return weight;
    }
    public int from() {    // 指出这条边的顶点
        return v;
    }
    public int to() {      // 这条边指向的顶点
        return w;
    }
    public String toString() {
        return String.format("%d->%d %.2f", v, w, weight);
    }
}

EdgeWeightedDigraph 类

public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");  // 换行
    private final int V;                // 顶点总数 
    private int E;                      // 边的总数
    private Bag<DirectedEdge>[] adj;    // 邻接表
    public EdgeWeightedDigraph(int V){
        this.V = V;
        this.E = 0;
        adj = (Bag<DirectedEdge>[]) new Bag[V];
        for(int v = 0; v < V; v++)
            adj[v] = new Bag<DirectedEdge>();
    }
    public EdgeWeightedDigraph(In in) {
        this(in.readInt());
        int E = in.readInt();
        for (int i = 0; i < E; i++) {
            int v = in.readInt();
            int w = in.readInt();
            double weight = in.readDouble();
            addEdge(new DirectedEdge(v, w, weight));
        }
    }
    public int V(){
        return V;
    }
    public int E(){
        return E;
    }
    public void addEdge(DirectedEdge e){  // 将 e 添加到该有向图中
        adj[e.from()].add(e);
        E++;
    }
    public Iterable<DirectedEdge> adj(int v) {  // 从 v 指出的边
        return adj[v];
    }
    public Iterable<DirectedEdge> edges(){  // 该有向图中的所有边
        Bag<DirectedEdge> bag = new Bag<DirectedEdge>();
        for(int v = 0; v < V; v++)
            for(DirectedEdge e : adj[v])
                bag.add(e);
        return bag;
    }

    public String toString() {  // 对象的字符串表示
        StringBuilder s = new StringBuilder();
        s.append(V + " " + E + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }
    public static void main(String[] args) {
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(new In());
        StdOut.println("----------------------");
        StdOut.println("加权有向图输出结果：");
        StdOut.println(G);
    }
}

运行结果：

最短路径 Dijkstra 算法