概述

一颗二叉搜索树可以为空，但如果不为空，必须满足以下性质：

• 非空左子树的所有键值小于其根结点的键值
• 非空右子树的所有键值大于其根结点的键值
• 左、右子树都是二叉搜索树

二叉查找树代码

public class BST<Key extends Comparable<Key>, Value> {
    private Node root;      // 二叉查找树的根结点
    private class Node{
        private Key key;    // 键
        private Value val;  // 值
        private Node left, right;   // 指向子树的链接
        private int size;  // 以该结点为根的子树中的结点总数

        public Node(Key key, Value val, int size) {
            this.key = key;
            this.val = val;
            this.size = size;
        }
    }
    .
    .
    .
}

二叉查找树操作

查找操作

在二叉查找树中查找一个键的递归算法：如果树是空的，则查找未命中；如果被查找的键和根结点的键相等，查找命中，否则我们就（递归地）在适当的子树中继续查找。如果被查找的键较小就选择左子树，较大则选择右子树。

代码

public Value get(Key key) {
    return get(root, key);
}

private Value get(Node x, Key key) {
    // 在以 x 为根结点的子树中查找并返回 key 所对应的值
    if (key == null) throw new IllegalArgumentException("calls get() with a null key");
    if (x == null) return null;
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) return get(x.left, key);
    else if (cmp > 0) return get(x.right, key);
    else              return x.val;
}

插入操作

插入方法的实现逻辑和递归查找很相似：如果树是空的，就返回一个含有该键值对的新结点；如果被查找的键小于根结点的键，我们会继续在左子树中插入该键，否则在右子树中插入该键。

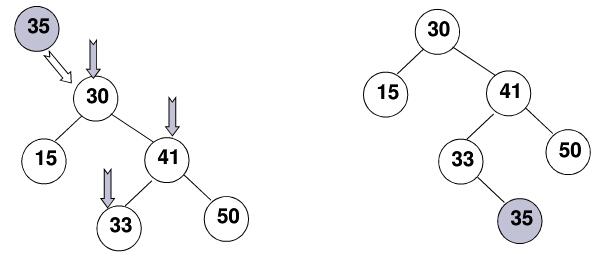
代码

public void put(Key key, Value val) {
    root = put(root, key, val);
}

private Node put(Node x, Key key, Value val) {
    // 如果key存在于为根结点的子树中则更新它的值
    // 否则将以key和val为键值对的新结点插入到该子树中
    if (x == null) return new Node(key, val, 1);
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) x.left  = put(x.left,  key, val);
    else if (cmp > 0) x.right = put(x.right, key, val);
    else              x.val   = val;
    x.size = 1 + size(x.left) + size(x.right);
    return x;
}

查找最小值和最大值

最小元素一定是在树的最左分支的端结点上；最大元素一定是在树的最右分支的端结点上。

// 最小值查找
public Key min() {
    return min(root).key;
} 

private Node min(Node x) { 
    if (x.left == null) return x; 
    else     return min(x.left); 
}

// 最大值查找
public Key max() {
    return max(root).key;
} 

private Node max(Node x) {
    if (x.right == null) return x; 
    else      return max(x.right); 
}

删除操作

deleteMin() 删除最小键

二叉查找树最难实现的方法就是 delete() 方法。作为热身运动，我们先考虑 deleteMin() 方法。最小键只能在左子树的端结点上，所以删除最小键 deleteMin 仅有以下两种情况。如下图所示，最小键就是 15 这个结点，它有两种情况：15 下面无子结点，15 下面有一个子结点（右子结点）。

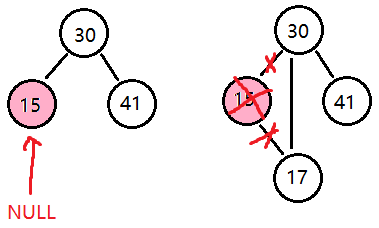
这两种情况的删除操作是非常容易实现的：若被删除结点无子结点，仅需将其置为 NULL 即可；若被删除的结点有一个子结点，仅需将其父结点指向其子结点即可，此时已经没有任何链接指向被删除的结点，因此它会被垃圾收集器清理掉。

代码

public void deleteMin() {
    root = deleteMin(root);
}

private Node deleteMin(Node x) {
    if (x.left == null) return x.right;
    x.left = deleteMin(x.left);
    x.size = size(x.left) + size(x.right) + 1;
    return x;
}

注意：deleteMax 和 deleteMin 是同理，所以就不再说明了。

delete() 删除操作

有了 deleteMin 操作的启示，我们可以用类似的方式删除任意只有一个子结点（或没有子结点）的结点，但应该怎样删除一个拥有两个子结点的结点呢？如下图所示。

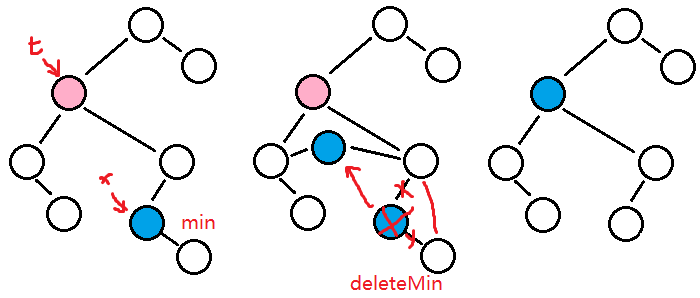
思路如下：

• 先找到被删除结点 t，再找 t 的右子树中最小结点或左子树最大结点 x，此案例是找右子树最小结点，用 min 实现
• 将 x 与 t 调换，t 位置就被 x 代替了，并仅需删除 x 原位置即可。这么做的好处是，由删除 t，变成了删除 x，而 x 是最小结点，所以仅一个或无子结点，此时删除操作就简单了，deleteMin 实现即可。

public void delete(Key key) {
    root = delete(root, key);
}

private Node delete(Node x, Key key) {
    if (x == null) return null;

    int cmp = key.compareTo(x.key);
    if      (cmp < 0) x.left  = delete(x.left,  key);
    else if (cmp > 0) x.right = delete(x.right, key);
    else { 
        if (x.right == null) return x.left;  // 一个或无子结点情况
        if (x.left  == null) return x.right;  // 一个或无子结点情况

        // 两个子结点情况
        Node t = x;
        x = min(t.right);
        x.right = deleteMin(t.right);
        x.left = t.left;
    } 
    x.size = size(x.left) + size(x.right) + 1; // 更新结点计数器
    return x;
}