二叉树的遍历

先序遍历

如上图所示，遍历过程

• 打印根结点
• 先序遍历其左子树
• 先序遍历其右子树

void preOrder(Node root){
    if(root != null){
        StdOut.print(root.item);
        preOrder(root.left);
        preOrder(root.right);
    }
}
// 时间复杂度 O(n)，空间复杂度 O(n)
// 最后输出 =》A B D F E C G H I

中序遍历

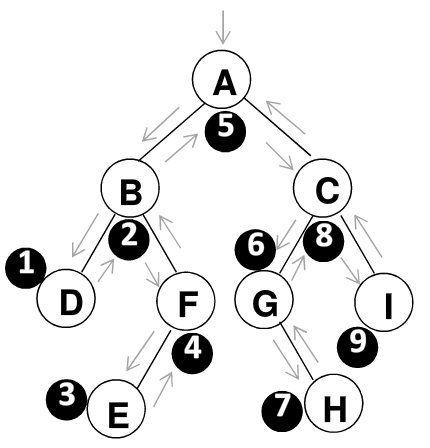
如上图所示，遍历过程

• 中序遍历其左子树
• 打印根结点
• 中序遍历其右子树

void inOrder(Node root){
    if(root != null){
        preOrder(root.left);
        StdOut.print(root.item);
        preOrder(root.right);
    }
}
// 时间复杂度 O(n)，空间复杂度 O(n)
// 最后输出 =》D B E F A G H C I

后序遍历

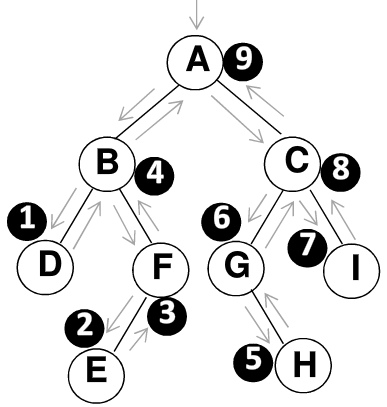
如上图所示，遍历过程

• 后序遍历其左子树
• 后序遍历其右子树
• 打印根结点

void postOrder(Node root){
    if(root != null){
        preOrder(root.left);
        preOrder(root.right);
        StdOut.print(root.item);
    }
}
// 时间复杂度 O(n)，空间复杂度 O(n)
// 最后输出 =》D E F B H G I C A

总结

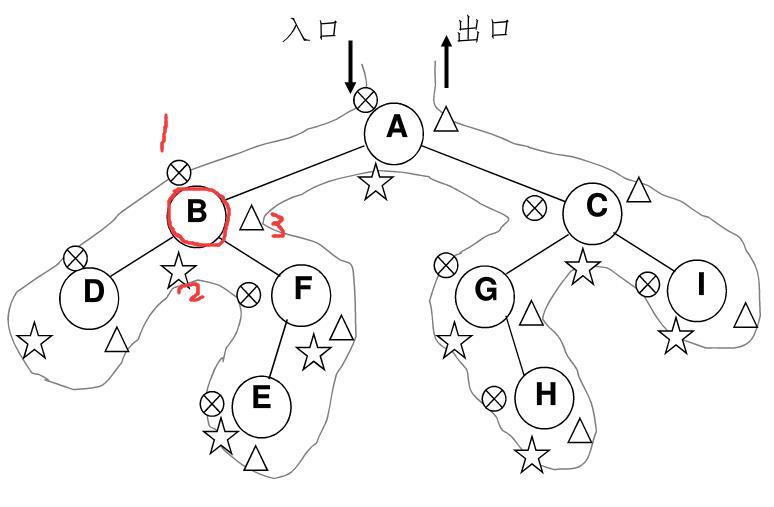
无论先序、中序、后序，他们遍历路径图都是一样的。唯一不一样的就是它们打印（访问）结点的时间。仔细看图，其实每个结点都有三次碰到它的机会。第一次是到结点；第二次是走完左子树回来；第三次是走完右子树回来。

如果第一次碰到结点就打印该结点，就是先序；第二次碰到再打印，就是中序；第三次碰到再打印，就是后序。

二叉树的非递归遍历

上述都是使用递归方式实现的，那么非递归算法实现的基本思路：使用堆栈。

先序遍历

遍历的过程

• 遇到一个结点，先访问结点，再把它压栈，并去遍历它的左子树
• 当左子树遍历结束后，从栈顶弹出这个结点
• 然后按其右指针再去先序遍历该结点右子树

void preOrderNonRecursive(Node root) {

    if(root == null) return;

    //这里采用java自带的Stack类，因为教程中写的堆栈类只能存 int 类型
    Stack<Node> s = new Stack<Node>();

    while(root != null || !s.isEmpty()){
        while(root != null ){
            StdOut.println(root.item);  /*遇到一个结点，直接打印（访问）它*/
            // 将其压栈，并去先序遍历它的左子树
            s.push(root); 
            root = root.left;        
        }
        if(!s.isEmpty())

            root = s.pop();  /*结点弹出堆栈*/
            root = root.right;  /*转向该结点右子树*/
    }

    return;
}

中序遍历

遍历的过程

• 遇到一个结点，就把它压栈，并去遍历它的左子树
• 当左子树遍历结束后，从栈顶弹出这个结点并访问它
• 然后按其右指针再去中序遍历该结点右子树

它与先序遍历不同就在于访问结点的时机不同，先序是一开始就访问，而中序需要左子树遍历结束后才访问。

void inOrderNonRecursive(Node root) {

    if(root == null) return;

    Stack<Node> s = new Stack<Node>();

    while(root != null || !s.isEmpty()){
        while(root != null ){
            s.push(root); 
            root = root.left;        
        }
        if(!s.isEmpty())
            root = s.pop(); 
            StdOut.println(root.item);  /*与先序遍历的唯一区别在这里*/
            root = root.right;
    }

    return;
}

后序遍历

后序遍历递归定义：先左子树，后右子树，再根节点。 后序遍历的难点在于：需要判断上次访问的节点是位于左子树，还是右子树。 所以它的遍历过程

• 若是位于左子树，则需跳过根节点，先进入右子树，再回头访问根节点
• 若是位于右子树，则直接访问根节点

public void postOrder(Node node){  
    if(node==null)  
        return;  
    Stack<Node> s = new Stack<Node>();  

    Node curNode; //当前访问的结点  
    Node lastVisitNode; //上次访问的结点  
    curNode = node;  
    lastVisitNode = null;  

    //把currentNode移到左子树的最下边  
    while(curNode!=null){  
        s.push(curNode);  
        curNode = curNode.item;  
    }  
    while(!s.empty()){  
        curNode = s.pop();  //弹出栈顶元素  
        //一个根节点被访问的前提是：无右子树或右子树已被访问过  
        if(curNode.right!=null&&curNode.right!=lastVisitNode){  
            //根节点再次入栈  
            s.push(curNode);  
            //进入右子树，且可肯定右子树一定不为空  
            curNode = curNode.right;  
            while(curNode!=null){  
                //再走到右子树的最左边  
                s.push(curNode);  
                curNode = curNode.left;  
            }  
        }else{  
            //访问  
            StdOut.println(curNode.item);  
            //修改最近被访问的节点  
            lastVisitNode = curNode;  
        }  
    } //while  
}

层序遍历

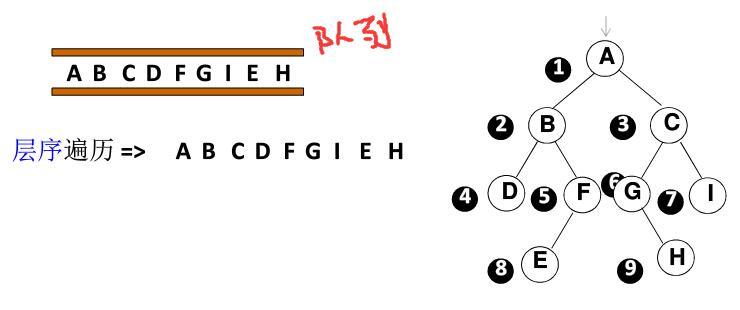
层序遍历是从上到下的层次遍历，且同一层是从左到右。可用队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队。

下例中初始时 A 入队。接下来 A 出队并访问它，其左右儿子 B、C 入队；B 出队并访问它，B 左右儿子 D、F 入队；C 出队并访问它 ... 以此类推，便可以遍历访问所有元素。

void levelOrder(Node root){

    BinaryTreeNode temp;
    // 采用java自带Queue的类，因为教程中写的队列类只能存 int 类型
    Queue<Node> q = new LinkedList<Node>();

    if(root == null){
        return;
    }

    q.offer(root); /*将根节点入队*/

    while(q.isEmpty()){

        temp = q.poll(); /*结点出队*/

        StdOut.println(temp.item);  /*访问该结点*/

        // 其左右儿子入队
        if(temp.left != null){
            q.offer(temp.left);  
        }

        if(temp.right != null){
            q.offer(temp.right);  
        }
    }
}